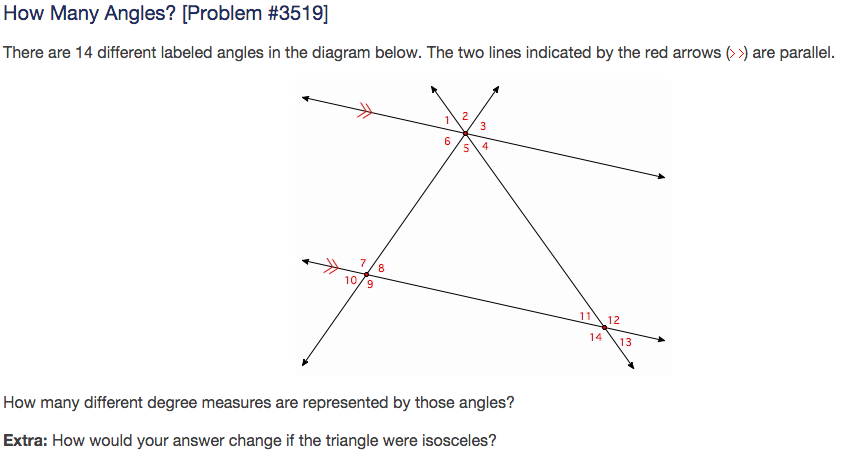
Every week, the Drexel University Math Forum web site poses a math question to their participants. Recently, the site asked their viewers to determine the measures of various angles formed by a pair of parallel lines and two transversals.

Orlee Marini-Rapoport, an eighth grade student in Kathryn Hill’s Geometry Honors class, used what she had learned in class to solve the problem. Her solution was one of those chosen to appear on the website as an example of a well-reasoned answer to the problem. Orlee used her knowledge of the vertical angles theorem and angles formed by a transversal intersecting two parallel lines to prove her conjecture.

Well done, Orlee!

 

Orlee’s solution:

There will be 5 different degree measures represented.

This goal is to find the angles that must be congruent to one another.

First, because I know that vertical angles are congruent, I identified which angles were congruent to which other angles using that theorem.

7 is congruent to 9
8 is congruent to 10
12 is congruent to 14
11 is congruent to 13
2 is congruent to 5
1 is congruent to 4
3 is congruent to 6

Because alternate interior angles are congruent, 8 is also congruent to 6 and therefore the measures of 8, 6, 10, and 3 are all equal. Also, 4 is congruent to 11, so the measures of 4, 11, 1, and 13 are all congruent.

So all in all:

4 = 11 = 1 = 13
8 = 6 = 3 = 10
7 = 9
12 = 14
2 = 5

The transversals aren’t parallel so there are no corresponding angles that could be congruent. (The measure of Angle 1 + the measure of Angle 2 is equals the measure of Angle 7, but no congruency there!)

After counting up the different measures, there are 5 different numbers represented.